3. INTERNAL BOUNDARY CONDITIONS

Since diffusion theory fails near the surface of a strong neutron absorber, a pair of group- and mesh-dependent effective diffusion parameters can be used to calculate reactivity effects of the absorber. An alternate approach is to isolate the absorber from the diffusion-theory calculation by applying group-dependent internal boundary conditions at the absorber surface.

The internal boundary condition, A, is of the form

D f¢ + A f = 0

where f¢ is the normal derivative of the flux at the absorber surface. Thus,

A = -D f¢ / f = J / f = D / d = l_tr / 3 d

where d º extrapolation distance into the absorber,

l_tr º the neutron transport mean free path in the diffusing medium, and

A º the internal boundary condition defined as the current-to-flux ratio at the

absorber surface.

Transport calculations are used to determine the group-dependent current-to-flux ratios. It is assumed that the material-dependent internal boundary condition is the same at every point on the surface of the absorber. However, current-to-flux ratios used in diffusion-theory calculations should never exceed the black absorber limit.

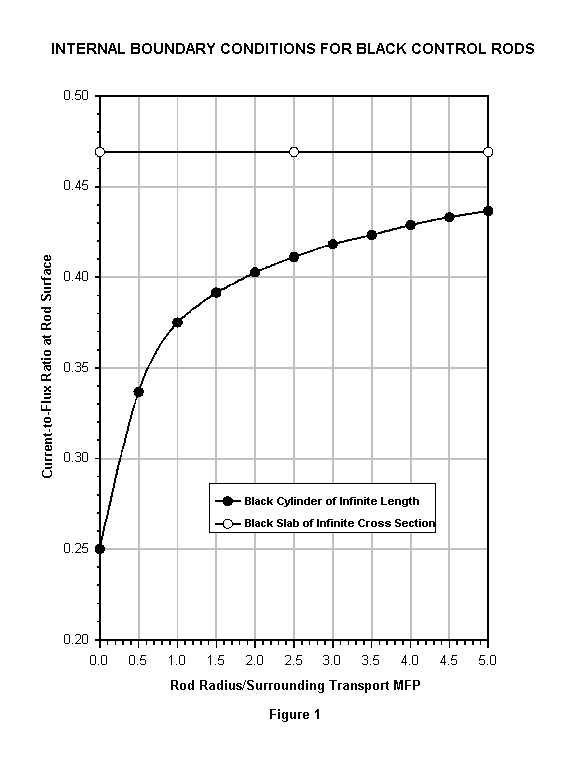
3.1 Current-to-Flux Ratios for Black Absorbers

For a plane black boundary (i.e. no return neutrons) the extrapolation distance has the value d = 0.7104l_tr which corresponds to a current-to-flux ratio A = l_tr / 3d = 0.4692. The extrapolation distance for a black cylindrical rod is a function of the radius, R, and the transport mean free path, l_tr , of neutrons in the surrounding medium. Figure 1 is a plot of the current-to-flux ratio evaluated at the surface of a black cylindrical absorber of infinite length as a function of R/l_tr .These black-rod internal boundary conditions were calculated from extrapolation distances given in Ref. 6. Note that in the limit as R/l_tr approaches infinity, the current-to-flux ratio becomes that of a planar black boundary. Using the least squares process, data from Fig. 1 were fit to a polynomial of the form

(J/f)_black = S _i a_i (R/l _tr)ⁱ

where the coefficients are:

	i	ai
	0	2.49993E-01
	1	2.50031E-01
	2	-1.87744E-01
	3	7.70505E-02
	4	-1.56659E-02
	5	1.00392E-03
	6	1.17961E-04
	7	-1.52381E-05

3.2 Current-to-Flux Ratios for Non-Black Absorbers

For non-black absorber materials the surface current-to-flux ratios are energy-dependent. For this case the internal boundary conditions can be calculated from a discrete-ordinate transport calculation using finely spaced mesh intervals in order to determine group-dependent fluxes and currents at the surface of the absorber. If any of the values exceed the values given in Fig. 1, they should be replaced with the black absorber limits. Internal boundary conditions are not needed for those upper energy groups for which S_a / S_s << 1 and/or t / L << 1 where L is the diffusion length and t is the minimum transverse dimension of the absorber material.

For the very special case of an absorber slab placed within a symmetric neutron field,
f_l = f_r and J_l = J_r. The surface current-to-flux ratio then equals the a blackness coefficient discussed earlier.

3.3 Example

Until recently, the shim-safety rods used in the University of Michigan Ford Nuclear Reactor consisted of a borated stainless steel material. Table 4 (from Ref. 5) gives the transverse dimensions and composition of these shim-safety rods. To obtain a set of internal boundary conditions, the rod, the surrounding moderator, and fuel were represented in cylindrical geometry. Since most thermal neutrons are absorbed near the surface of the shim-safety rod, the radius of the "equivalent" cylindrical rod was chosen so as to preserve the surface area of the actual rod. This cylindrical rod was divided into three concentric zones with the outer and middle zones having thicknesses of 1 mm and
3 mm, respectively. Full-density borated stainless steel was used in the outer and middle zones, but the density in the inner zone was reduced so as to preserve the total amount of material in the equivalent rod. Multigroup cross sections were generated for each control zone and for all the other regions outside the shim rod using the WIMS-D4M code⁷. One-dimensional P₁ S₈ transport calculations were performed with the TWODANT code⁸ in order to determine group-dependent current-to-flux ratios on the surface of the equivalent cylindrical rod. Table 5 summarizes the current-to-flux ratios obtained in this manner. This table also shows the internal boundary conditions calculated for the TiB₂(95% ¹⁰B)-Al6351 shim rods now used in the Ford Nuclear Reactor. Based on S_a / S_s, t / L, and S_at values, where t is the minimum thickness of the actual shim rod, Table 5 shows that internal boundary conditions are not needed for the fast groups 1 and 2 and that the rod is black to group-4 neutrons. Therefore, the polynomial fit to Fig. 1 was used to determine the group-4 current-to-flux ratios.

TABLE 4 COMPOSITION AND GEOMETRY OF THE FNR SHIM-SAFETY RODS
Composition (atoms/b-cm)
Nuclide	Borated Stainless Steel	TiB2(95%10B)-Al6351
10B	1.108E-3	1.5749E-3
11B	5.184-3	7.5390E-5
Mg		4.0978E-4
Al		5.7161E-2
Si		5.9104E-4
Ti		1.0158E-3
V		1.6293E-5
Cr	1.640E-2	1.5962E-5
Mn		1.8129E-4
Fe	5.644E-2	1.4862E-4
Ni	1.130E-2	1.4131E-5
Cu		2.6122E-5
Zn		5.0734E-5
Geometry
Dimensions (cm)		Borated SS	TiB2-Al6351
Effective Length		60.960	60.960
Rectangular-Like Cross Section
Major Axis		5.668	5.715
Minor Axis		2.198	2.222
Radius of Rounded Ends		1.099
Radius of Rounded Corners			0.635

TABLE 5 INTERNAL BOUNDARY CONDITIONS FOR THE FNR SHIM-SAFETY RODS
Borated Stainless Steel Rods
Quantity	Group 1	Group 2	Group 3	Group 4
Eu(eV)	1.0000E+07	8.2100E+05	5.5300E+03	6.2500E-01
Sa/Ss	6.8727E-03	6.4574E-03	1.5990E-01	2.6788E+00
D(cm)	1.6583E+00	8.8032E-01	3.1743E-01	9.5010E-02
Sa(cm-1)	1.8958E-03	3.3825E-03	1.4756E-01	2.5676E+00
L(cm)	2.9576E+01	1.6132E+01	1.4667E+00	1.9236E-01
t/L	7.4318E-02	1.3625E-01	1.4986E+00	1.1426E+01
Sat	4.1669E-03	7.4347E-03	3.2434E-01	5.6436E+00
IBC = J/f	2.5331E-02	-1.1123E-02	8.1122E-02	4.0956E-01
TiB2(95%10B)-Al6351 Rods
Sa/Ss	3.6927E-03	1.4154E-02	1.7049E+00	3.7923E+01
D(cm)	3.1275E+00	1.6415E+00	1.1959E+00	9.3876E-02
Sa(cm-1)	6.6305E-04	3.6092E-03	1.7942E-01	3.4624E+00
L(cm)	6.8680E+01	2.1326E+01	2.5818E+00	1.6466E-01
t/L	3.2360E-02	1.0422E-01	8.6082E-01	1.3498E+01
Sat	1.4736E-03	8.0214E-03	3.9876E-01	7.6952E+00
IBC = J/f	1.3262E-02	-6.9260E-03	1.1656E-01	4.1097E-01

NOTE: These tables show that:

1. IBC's are not needed for groups 1 and 2 since S_a/S_s <<1.

2. IBC's are needed for groups 3 and 4.

3. IBC for group 4 is that of a black rod since S_at >>1.