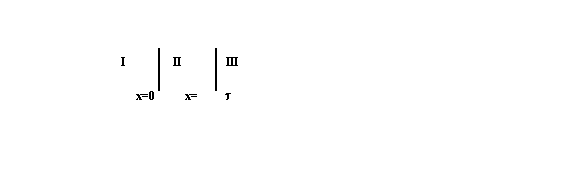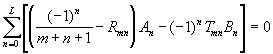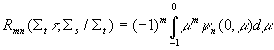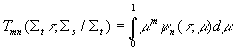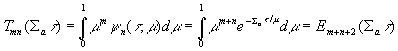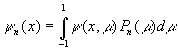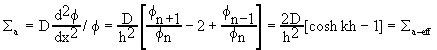APPENDIX

Blackness Coefficients and Effective Diffusion Parameters in Slab Geometry

Mesh-dependent effective diffusion parameters are often used to calculate control rod worths within the limitations of diffusion theory. For slab absorbers these effective diffusion parameters are functions of a pair of blackness coefficients. This appendix illustrates a method for calculating the blackness coefficients in the P₁ approximation with and without scattering in the absorber slab and discusses how the method may be extended to the P₃ and P₅ approximations. Equations are derived for the effective diffusion parameters as functions of the blackness coefficients and the mesh interval size within the absorber.

A.1 Matching Conditions on the Absorber Surfaces

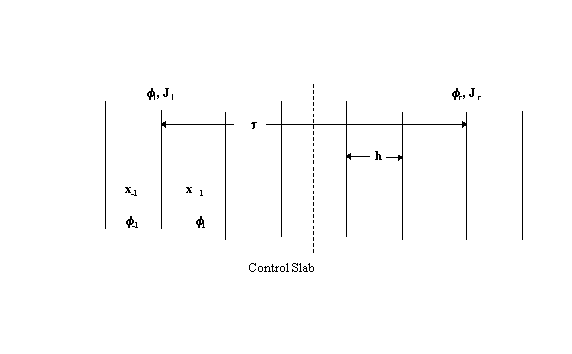
Consider the three-region slab configuration shown below.

The absorber region (Region II) extends from x=0 to x=t and is assumed to be a source-free region which scatters neutrons isotropically. Since the angular fluxes y(x,m) incident on Region II from Regions I and III must be continuous at the boundaries,

y_II(0,m) = y_I(0,m), m >0

y_II(t,m) = y_III(t,m), m<0

where is the cosine of the angle between the flux direction and the normal to the slab. The boundary fluxes in Regions I and III may be expanded into a power series over the range of m (-1 to 1). Thus,

Maynard (Ref. 1) has shown that the angular flux continuity requirement leads to the matching conditions

and

if the absorber (Region II) is source-free and scatters neutrons isotropically. It turns out that either the even or odd moments can be matched. The odd moments are usually chosen. Thus, only odd values of m are used in these matching equations with m_max = L. R_mn and T_mn are reflection and transmission coefficients defined by the equations

R_mn and T_mn are the reflected and transmitted contributions to the outgoing m_th moments due to the incoming flux. They are defined to be positive and are functions only of the absorber thickness (t) and its macroscopic scattering and absorption cross sections (S_s and S_a).

A.2 Evaluation of the Reflection and Transmission Coefficients

For the purpose of evaluating R_mn and T_mn it is convenient to assume that Regions I and III are voids and that a mⁿ (n=0,1,2,...) source distribution is incident on the absorber slab from the left. For this source distribution the monoenergetic one-dimensional Boltzmann transport equation is solved for the surface angular fluxes y_n(0,m) and y_n(t,m). Using the one-dimensional option of the TWODANT code⁸ (i.e. ONEDANT), an angular quadrature of 24 (S₂₄), and double P_N quadrature constants, R_mn and T_mn can be readily integrated by the Gauss-Legendre quadrature method. Thus,

,

m<0

,

m>0

where N is the angular quadrature order (S_N) and W_i are the required Gauss-Legendre weights which are normalized so that in the range from i=1 to i=N/2 they sum to unity. The abscissas (m_i) and weights (W_i) are given below for N=24.

	Abscissas	Weights
	±0.99078	0.023588
	±0.95206	0.053470
	±0.88495	0.080039
	±0.79366	0.101580
	±0.68392	0.116750
	±0.56262	0.124570
	±0.43738	0.124570
	±0.31608	0.116750
	±0.20634	0.101580
	±0.11505	0.080039
	±0.04794	0.053470
	±0.00922	0.023588

 

For the special case of a pure absorber slab (S_s = 0) R_mn is zero and T_mn can be easily evaluated. For this case the transmitted angular flux is the product of the incident flux mⁿ and the probability of a neutron passing through the slab without absorption (e^-Sat/m ). Thus,

where E_m+n+2 (S_at) is the exponential integral of order m+n+2.

A.3 Evaluation of the Blackness Coefficients

In the regions outside the control blade the angular fluxes satisfy the monoenergetic, one-dimensional, time-independent Boltzmann transport. To obtain analytical expressions for the blackness coefficients the angular fluxes on the surfaces of the absorber are expanded into a series which in the P_L approximation becomes

where y_n(x) is the nth spherical harmonic moment and where P_n(m) is the nth Legendre polynomial. The spherical harmonic moments are given by the equation

Although the higher order moments are more complicated, y₀(x) and y₁(x) are just the neutron flux and neutron current, respectively.

In the P₁ approximation (L=1=m) the angular fluxes on the left-hand and right-hand surfaces of the absorber plate become

Similarly,

Hence, , , , .

Note that B₁ is negative because the blackness coefficients are defined in terms of currents into the absorber slab. Adding the Maynard matching equations for the L = 1 case gives

Using the above values for (A₀ + B₀) and (A₁ - B₁) this equation becomes

The blackness coefficient in the P₁ approximation is therefore

.

Using the same procedure but subtracting the Maynard matching equations gives the blackness coefficient.

Note that the b-equation can be obtained from the a-equation by simply changing the sign of the transmission coefficients. This is a general result which is also valid in the P₃ and P₅ approximations.

As discussed above, for the case of zero scattering the reflection coefficients vanish and the transmission coefficients reduce to exponential integrals. Thus, the no-scattering P₁ approximation for the blackness coefficients becomes

.

Recall that improved values are obtained for these blackness coefficients by using the modified forms (a_0m and b_0m) in which the (1/2) coefficient is replaced with the value 0.4692.

These P₁ approximations for the blackness coefficients show that they are functions only of the properties of the absorber slab (S_a, S_s, and t). This is also true for the higher order approximations. Although the algebra is tedious, these same methods can be used to find the blackness coefficients in the P₃ and P₅ approximations. However, for these cases the spherical harmonic moments y_n(x) need to be evaluated on the surfaces of the control slab for n=2,3,4 and 5.

To calculate these higher-order spherical harmonics it is assumed that the control blade is surrounded by an homogenized fuel zone. For this medium the monoenergetic, one-dimensional, time-independent Boltzmann equation is multiplied by (2n + 1)P_n(m) and integrated over all m. Using the recurrence relation

(n + 1)P_n+1(m) + nP_n-1(m) = (2n + 1)mP_n(m) ,

this integration leads to a set of first-order coupled differential equations for the spherical harmonics which, in the P_L approximation, are subject to the requirement that y_n(x) = 0 for n>L. Solutions to these differential equations are of the form

y_n(x) = g_n(n) e^nx/l

where l is the total mean free path of neutrons in the homogenized fuel regions outside the absorber slab. Substituting this solution into the differential equations for the spherical harmonics leads to a recurrence relation for the g_n(n)'s with g₀(n) defined to be unity. In the P_L approximation y_L+1(x) = 0 which requires g_L+1(n) = 0. This condition leads to the allowed values of n which are positive and which are (L-1)/2 in number. Recall that in the P_L approximation only odd values of L are used. Since the blackness coefficients are functions only of the properties of the absorber slab, it is necessary to assume that the surrounding fuel regions are infinite in extent (no leakage) with either isotropic or linear anisotropic scattering.

Following these procedures Ref. 3 shows that

g₀(n) = 1

g₁(n) = 0

g₂(n) = -1/2

g₃(n) = 5/(6n)

g₄(n) = 3/8 - 35/(24n²)

g₅(n) = -[9g₄(n) + 4 n g₃(n)]/(5n)

g₆(n) = -[11g₅(n) + 5 n g₄(n)]/(6n)

In the P₃ approximation there is one allowed n-value since (L-1)/2 = 1 and this value is obtained from the requirement that g₄ = 0. Thus, n₂(P₃) = (35)^1/2/3. Similarly, in the P₅ approximation n₂(P₅) = 1.2252109 and n₃(P₅) = 3.2029453. These values of n and g_n(n) determine the higher order spherical harmonics evaluated on the absorber slab surfaces. Thus,

Spherical Harmonics in the P3 Approximation

	y0l = fl + a2	y0r = fr + b2
	y1l = Jl	y1r = - Jr
	y2l = g2(n2) a2	y2r = g2(n2) b2
	y3l = g3(n2) a2	y3r = - g3(n2) b2

Spherical Harmonics in the P5 Approximation

	y0l = fl + a2 + a3	y0r = fr + b2 + b3
	y1l = Jl	y1r = - Jr
	y2l = g2(n2) a2 + g2(n3) a3	y2r = g2(n2) b2 + g2(n3) b3
	y3l = g3(n2) a2 + g3(n3) a3	y3r = - g3(n2) b2 - g3(n3) b3
	y4l = g4(n2) a2 + g4(n3) a3	y4r = g4(n2) b2 + g4(n3) b3
	y5l = g5(n2) a2 + g5(n3) a3	y5r = - g5(n2) b2 - g5(n3) b3

 

where a₂, a₃, b₂, and b₃ are arbitrary constants which are eliminated in the evaluation of the blackness coefficients.

With these values for the spherical harmonics the blackness coefficients can be calculated in the P₃ and P₅ approximations following the same approach as was used above for the P₁ approximation. As before, the continuity requirement of the angular fluxes at the surfaces of the absorber slab determines the expansion coefficients A_n and B_n in terms of the spherical harmonics y_nl and y_nr. To determine the blackness coefficient a in the P₃ approximation, for example, Maynard's matching equations are added together for m=1 and for m=3. From these two equations the constant (a₂ + b₂) is eliminated and from the resulting equation a(P₃) is determined. By subtracting the equations and eliminating the constant (a₂ - b₂), b(P₃) is obtained. b(P₃) can also be found by simply changing the sign of all the transmission coefficients (T_mn) in the final expression for a(P₃).

Although the algebra is very tedious, the same procedure is used to find a(P₅) and b(P₅). For this case Maynard's two matching equations are added together for m=1, m=3, and m=5. From these three equations the constants (a₂ + b₂) and (a₃ + b₃) are eliminated and the resulting equation solved for a(P₅). Changing the signs of the reflection coefficients in this equation determines b(P_5.).

For more details regarding these procedures see Ref. 3. As for the P₁ case, the P₃ and P₅ blackness coefficients are functions only of the properties of the absorber slab (t, S_a, and S_s).

A.4 Evaluation of the Effective Diffusion Parameters

The effective diffusion parameters are chosen so as to preserve the current-to-flux ratios on the surfaces of the control slab as given by the blackness coefficients. Since these effective diffusion parameters are to be used in a finite difference solution of the diffusion equation, they contain an explicit dependence on the mesh interval size, h. This allows the use of a very coarse mesh in the absorber for diffusion calculations. Equations will be derived for the effective values of D and S_a for use in those diffusion codes, such as DIF3D⁴, which evaluate fluxes at the center of mesh intervals. The same methods may be used to determine the effective diffusion parameters for codes which evaluate fluxes on mesh interval boundaries. These techniques for determining mesh-dependent effective diffusion parameters as functions of a and b were first proposed by E. M. Gelbard.¹⁷

Consider the following diagram.

It is convenient to assume that the same material extends to regions outside the absorber slab of thickness t. Since a and b depend only on the properties inside the slab, this assumption leads to no loss in generality. If the flux varies linearly from the center to the edge of the mesh cell,

f_l = (f_-1 + f₁)/2 and J_l = (D/h)(f_-1 - f₁) .

The solution to the diffusion equation within the source-free absorber consists of a symmetric (cosh kx) part and an asymmetric (sinh kx) part with respect to the centerline. For the symmetric solution, f_l = f_r , J_l = J_r , f₁ = C cosh k(t - h)/2, and f_-1 = C cosh k(t + h)/2 so that after some manipulation

Similarly, for the asymmetric solution, J_l = -J_r, f_l = -f_r, f₁ = A sinh k(t - h)/2, f_-1 = A sinh k(t + h)/2 so that

.

The ratio of these equations gives

from which it follows that

.

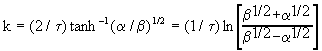
The expression for the effective diffusion coefficient is obtained by adding the equations for a and b.

An expression for the effective macroscopic absorption cross section is obtained by writing the diffusion equation for the control slab in finite difference form and solving for S_a. Thus,

where

f_n = C cosh kx_n

f_n+1 = C cosh k(x_n + h)

f_n-1 = C cosh k(x_n - h) .

These equations for k, D, and S_a determine the effective diffusion parameters in terms of the blackness coefficients (a and b) and the mesh interval size h for the case of mesh-centered fluxes.

The same procedures can be used to find the effective diffusion parameters for diffusion codes which evaluate fluxes on mesh boundaries. The results for k and S_a are the same as those given above. However, the expression for the effective diffusion coefficient becomes

D_eff .

For greatest accuracy the effective diffusion parameters should be evaluated using the spectrum-weighted blackness coefficients <a(P₅)> and <b(P₅)>.